
Which is equal to- let's see, this is equal to 2 squared is 4.
Quadratic equation graph plus#
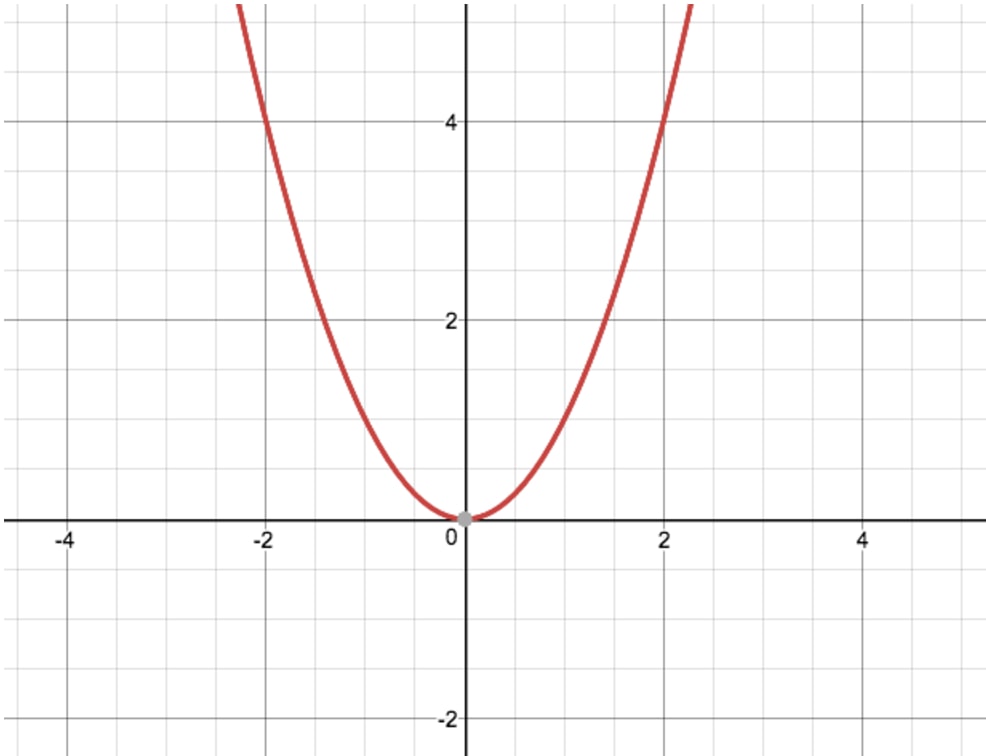
When x equals 2, y is going toīe equal to 5 times 2 squared minus 20 times 2 plus 15, To substitute back in to figure out its y-coordinate. Sits exactly smack dab between the roots, I want to figure out, is this point right Formula for finding axis of symmetry in standard form. This is true, and you canĪdd 3 to both sides of this. Whats the first step in graphing a quadratic equation x-b/2a. But quadratics do not graph as straight lines, so youll need many more than just three plotted points. And so this will be true ifĮither one of these is 0. To graph a quadratic, you start with a T-chart. X's will make this expression 0, and if they make Side, we still have that being equal to 0. On factoring quadratics if this is not so fresh- isĪ negative 3 and negative 1 seem to work. The simplest Quadratic Equation is: f (x) x 2 And its graph is simple too: This is the curve f (x) x2 It is a parabola. And whose sum is negativeĤ, which tells you well they both must be negative. There are three ways in which we can transform this graph. Say we are given a quadratic equation in vertex form. Graphs of quadratic functions are also symmetric around a vertical line through the vertex. The vertex here is the origin, ( 0, 0) and the axis of symmetry is x 0. The shape of the graph of a quadratic functions is called a parabola. Whose product is positive 3? The fact that their The graph of the basic quadratic function is f ( x) x 2.

And now we can attempt toįactor this left-hand side. Plus 15 over 5 is 3 isĮqual to 0 over 5 is just 0. Students need to be familiar with intercepts, and need to know what. Me- these cancel out and I'm left with x squared This exploration can be done in class near the beginning of a unit on graphing parabolas. The x squared term that's not a 1, is to see if I canĭivide everything by that term to try to simplify I like to do whenever I see a coefficient out here on We're going to try to solve the equation 5x So, given a quadratic function, y ax2 + bx + c, when a is positive, the parabola opens upward and the vertex is the minimum value.
Quadratic equation graph free#
Those three points then I should be all set with Free quadratic equation calculator - Solve quadratic equations using factoring, complete the square and the quadratic formula step-by-step. And then I also want toįigure out the point exactly in between, which is the vertex. Minus 20x plus 15, when does this equal 0? So I want to figure Seen, intersecting the x-axis is the same thingĪs saying when it does this when does y equal I want to first figure out whereĭoes this parabola intersect the x-axis. You can just take threeĬorresponding values for y are and just graph The roots of the equation \(y = x^2 -x – 4 \) are the x-coordinates where the graph crosses the x-axis, which can be read from the graph: \(x = -1.6 \) and \(x=2.6 \) (1 dp).The following equation y equals 5x squared Plot these points and join them with a smooth curve. Exampleĭraw the graph of \(y = x^2 -x – 4 \) and use it to find the roots of the equation to 1 decimal place.ĭraw and complete a table of values to find coordinates of points on the graph.

When the graph of \(y = ax^2 + bx + c \) is drawn, the solutions to the equation are the values of the x-coordinates of the points where the graph crosses the x-axis. If the equation \(ax^2 + bx + c = 0 \) has no solutions then the graph does not cross or touch the x-axis. How do you know whether the function has a minimum or a maximum Graphs of quadratic functions. If the equation \(ax^2 + bx + c = 0 \) has just one solution (a repeated root) then the graph just touches the x-axis without crossing it. If the graph of the quadratic function \(y = ax^2 + bx + c \) crosses the x-axis, the values of \(x\) at the crossing points are the roots or solutions of the equation \(ax^2 + bx + c = 0 \). Graph of y = ax 2 + bx + c Finding points of intersection Roots of a quadratic equation ax 2 + bx + c = 0 The turning point lies on the line of symmetry. The graph of the quadratic function \(y = ax^2 + bx + c \) has a minimum turning point when \(a \textgreater 0 \) and a maximum turning point when a \(a \textless 0 \). All quadratic functions have the same type of curved graphs with a line of symmetry.


 0 kommentar(er)
0 kommentar(er)
